庭の一画に自転車置き場を作っている。
ここに作ろうと決めた場所には2本の木が生えていたので、引っこ抜いて別の場所に移設した。
どちらも華奢な木で、移設は簡単だったけれど、それでも1時間くらい使うのは面倒くさい。「誰がこんなところに植えたんだよ。俺だよ」というのを、ひとりで2回やった。
木が無くなったところに、敷地の長方形を決める。
といっても、なんの目印もないところに、フリーハンドで長方形は書けない。
なぜか。
直角を出せないからだ。
さて、どうするか。
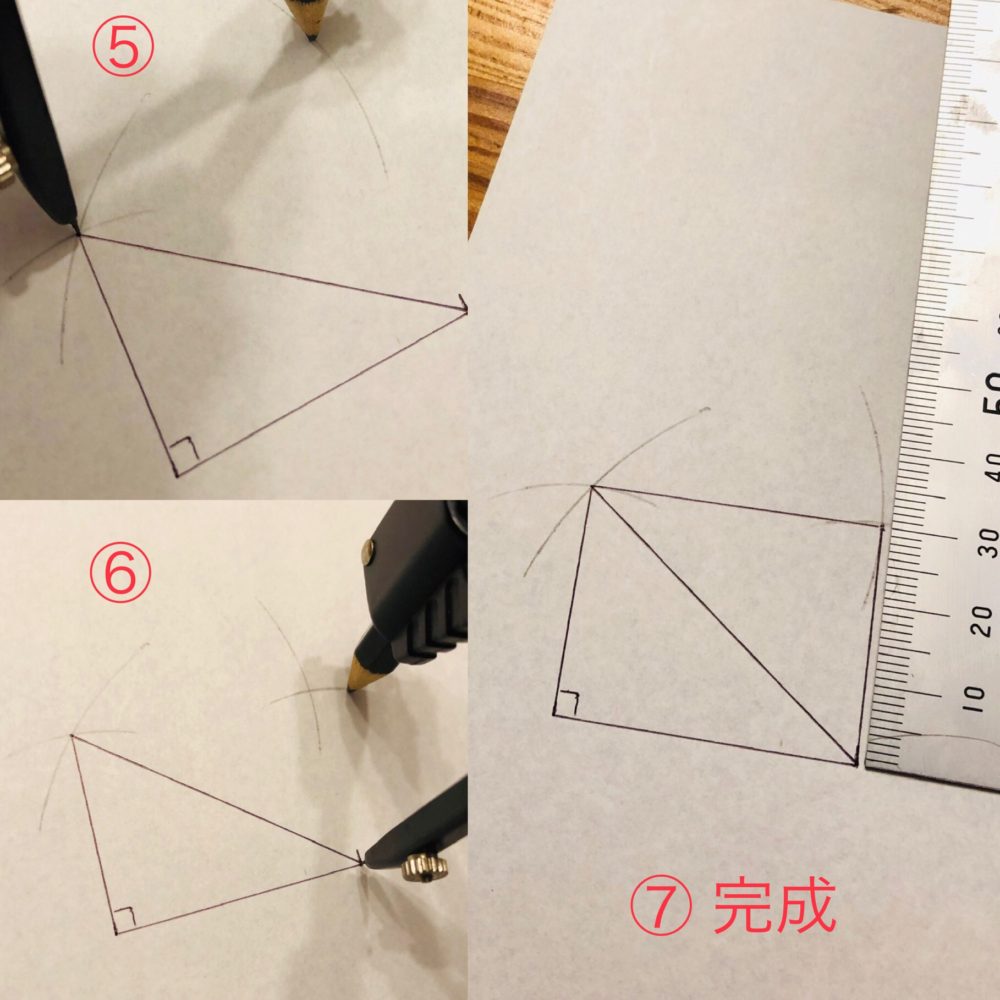
ここで、建築の職人さん達が使う「さしご」の法則を用いる。「さしご」とは「3:4:5」、三角形の三辺の比率を3:4:5にすると直角三角形になるというもの。そう、これはあのピタゴラスの定理(直角三角形の底辺の2乗と高さの2乗の合計は、斜辺の2乗に等しい)に当てはまる。最初に4の長さの線を引き、その両端から3の長さと5の長さで弧を描く。弧が交わる点と4の線の両端を結べば直角三角形ができる。その斜辺を使って対の三角形を作れば、長方形ができる。
作業中の写真がないので、コンパスで再現してみた。
なぜこうなるのか。不思議で仕方がない。学生時代、アルバイト先の建築現場で僕に「さしご」を教えてくれた職人さんは「なんでこうなるか教えてやろうか?ええか?これはな、そういうもんなんじゃ」と言っていた。なんだそれ、とその時は思ったけれど、何度やってもそうなるから、そういうもんなんだろう。それにしても、これはすごい。直角を出すときに、便利すぎるのだ。この定理を中学校で習った時はなんとも思わなかったのに、大学時代のアルバイト先や、大人になって庭で「さしご」を使って長方形を描きながら「そういうもん」に感動するのは、なんだか間抜けである。しかし仕方がない。そういうもんだ。
敷地に長方形を出したら、次は四隅に脚を立てるための土台をセットする。寸法を決めた脚を立ててその上に屋根を付けるので、土台は同じ高さにセットされなければならない。
といっても、なんの目印もないのに、フリーハンドで土台の高さは統一できない。
なぜか。
水平を出せないからだ。
さて、どうするか。
プロはレーザー水平器という便利な機械で水平を出すけれど、僕は持っていない。
ここで、建築の職人さん達が昔使っていた「水盛り」という方法を用いる。
適当な深さの穴を4つ掘り、基礎ブロックを置く。その脇に杭を打っていく。基準にするブロックに水の入ったペットボトルを置いて、そこから透明なホースを伸ばす。それを端から吸う。ホースの中の水位は、重力の関係(サイフォンの原理)でペットボトルの中の水位と常に同じになる。ホースを持ってそれぞれの杭に印をつけて回り、それらを糸で結べば水平面が出せる。この水平面を基準に穴の深さを調整してブロックを置けば、全てのブロックの高さが同じになる。
作業中に撮った写真が少なくてわかりにくいので、室内で再現してみた。
なぜこうなるのか。不思議で仕方がない。この法則も学生の時に習ったんだろうか。と、ググってみると、サイフォンの原理は沢山のサイトで説明されている。ただ、僕はどれを読んでも、よくわからない。でもいいのだ。文章や数式による細かい説明がわからなくても、ホースの中の水面がゆっくりと動いてやがてピタッと止まるのを見たり、それを使って自ら庭の4箇所に水平にブロックを設置したりすれば、そういうもんだということは、よくわかる。
こうして、庭の一画に長方形の敷地を決め、その四隅に水平にブロックを設置した。「さしご」と「水盛り」で直角と水平・・・便利すぎる。と、ひとり唸るのであった。
ところで僕らはなぜ、直角や水平を基準にモノを作ろうとするのか。見渡せば、テレビやパソコンの画面、本、道路、建物、牛乳パック・・・もう全てである。なんだこれは。よくわからんが、これもやはり「そういうもん」だろう。大昔に誰かが、水たまりの水面や長く伸びた影、物が上から下に落ちる様子を見て「あっ、なんか、まっすぐだ」と思って、その友達に「まっすぐって、いいね?」とか言ったんじゃないか。植物のツルをいくつも繋げて紐状にしたものを友達と引っ張って「これ、こっからここまでが俺んちだから!とかやるときに、便利だよね?」とか「たいらなところって、リンゴが転がらないから、いいね」とか言ってたんだろうな。大昔からそういうやりとりが何万回と繰り返されて、いろんな「そういうもん」ができたんだろうな。
そんなことを、時々考える。そんな暇があったら、仕事か、何か資格の勉強でもした方がいいのかもしれない。でも、時々おもしろいことがあるから、つい考えてしまう。図形や空間の性質を研究する「幾何学(geometry)」という学問の名前が、 geo(土地) と metry(測る:メートルの起源)という二つの言葉が組み合わさって出来ていると知った時には、おっ、これは「こっからここまでが俺んちだから!」のことじゃないか、と思った。自分の想像と言葉の由来、2つの点と点がピンと張った直線で繋がったような気がして、とても気持ち良かった。
そんなことを考えているうちに巡り合った、考古学者・樋口清之の著書『日本人はなぜ 水に 流したがるのか』に、こんな一節があった。
日本人は水を絶えず眺めて暮らす水田農耕者だった。われわれの祖先はこのように水田を眺めることで、まず、水平面を発見する。水田の基本となる水平面に対して確固たる目をもたなくては、隣の水田とのトラブルをいつも抱えなくてはならないからである。
自然水の水平面の高低差が隣接水田との間に水を流すことになるので、水平に対する観察は相当緻密で正確を期したのである。
水平を見つけると、垂直を見つけるのは早かった。
水平である田んぼに降る雨はときとして垂直に落ちる。
日本人は、水田を見つめ続けて水平と垂直を早くに見つけたのである。これは、現在のわれわれから考えると一見なんでもないことのように思えるかもしれないが、水平、垂直の発見が早いか遅いかで文化は大きく差が開き、のちの測量技術を正確に発展させるかどうかのわかれ目になっていくのである。
樋口清之 (1989) 『日本人はなぜ 水に 流したがるのか』 MG出版 P144より
なんと、これは日本版の「こっからここまでが俺んちだから!」じゃないか。これを読んだ時、僕は胸熱の極みだった。
>>>
庭の木を抜き、地面の1か所に基準点を決め、最初に引いた4の長さの線から長方形ができた。その四隅のブロックに水平ができた。点が線に、線が面になった。だけじゃない。実は目に見えない線もたくさん伸びている。いろんなことが、つながっていくのが、たまらない。
・・・と、考えているうちに我に返る。
おい俺、はよ作れ。
自転車置き場は今、脚部まで組み上がったところ。その骨組みは、娘たちの遊具と化している。
彼女たちが飽きるまでは、しばらくこのままにしておく。
続編はコチラ>>












コメントを投稿するにはログインしてください。